Velocity Can Only Be Described by Including Both

Speed and direction of a move

Velocity
As a alter of direction occurs while the racing cars turn on the curved track, their velocity is not constant.
Common symbols	$v$ , $v$ , $v$ →
Other units	mph, ft/southward
In SI base of operations units	m/s
Dimension	L T ⁻¹

The velocity of an object is the charge per unit of change of its position with respect to a frame of reference, and is a function of time. Velocity is equivalent to a specification of an object'south speed and direction of motion (e.g. 60 km/h to the due north). Velocity is a cardinal concept in kinematics, the branch of classical mechanics that describes the motion of bodies.

Velocity is a physical vector quantity; both magnitude and management are needed to define it. The scalar absolute value (magnitude) of velocity is chosen speed, being a coherent derived unit whose quantity is measured in the SI (metric system) as metres per 2d (chiliad/s or m⋅s⁻¹). For example, "five metres per second" is a scalar, whereas "5 metres per 2nd due east" is a vector. If at that place is a change in speed, direction or both, and so the object is said to be undergoing an dispatch.

Constant velocity vs acceleration

To have a constant velocity, an object must have a constant speed in a constant direction. Constant direction constrains the object to motion in a straight path thus, a constant velocity ways motion in a directly line at a constant speed.

For example, a car moving at a constant xx kilometres per 60 minutes in a circular path has a constant speed, simply does not take a constant velocity considering its direction changes. Hence, the car is considered to be undergoing an acceleration.

Departure between speed and velocity

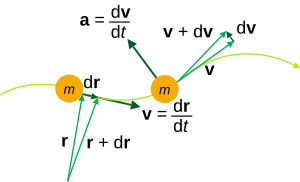
Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.

Speed, the scalar magnitude of a velocity vector, denotes only how fast an object is moving.^[1] ^[2]

Equation of move

Average velocity

Velocity is defined equally the rate of change of position with respect to fourth dimension, which may as well be referred to as the instantaneous velocity to emphasize the distinction from the average velocity. In some applications the average velocity of an object might be needed, that is to say, the constant velocity that would provide the aforementioned resultant displacement equally a variable velocity in the same time interval, $5 (t)$ , over some time menses $Δ t$ . Average velocity can be calculated as:

{\boldsymbol {\bar {v}}}={\frac {\Delta {\boldsymbol {x}}}{\Delta t}}.

The average velocity is always less than or equal to the average speed of an object. This tin be seen by realizing that while distance is always strictly increasing, deportation can increase or decrease in magnitude as well equally change direction.

In terms of a displacement-time (x vs. t) graph, the instantaneous velocity (or, simply, velocity) can be idea of every bit the slope of the tangent line to the curve at any point, and the average velocity as the slope of the secant line between 2 points with t coordinates equal to the boundaries of the fourth dimension menses for the average velocity.

The average velocity is the same as the velocity averaged over time – that is to say, its time-weighted average, which may be calculated every bit the time integral of the velocity:

{\boldsymbol {\bar {v}}}={1 \over t_{1}-t_{0}}\int _{t_{0}}^{t_{1}}{\boldsymbol {v}}(t)\ dt,

where we may identify

\Delta {\boldsymbol {x}}=\int _{t_{0}}^{t_{1}}{\boldsymbol {v}}(t)\ dt

and

\Delta t=t_{1}-t_{0}.

Instantaneous velocity

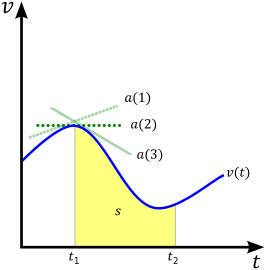
Example of a velocity vs. time graph, and the relationship between velocity v on the y-axis, acceleration a (the three green tangent lines correspond the values for dispatch at different points along the curve) and displacement s (the yellowish surface area under the bend.)

If we consider $v$ every bit velocity and $x$ every bit the displacement (change in position) vector, then we can express the (instantaneous) velocity of a particle or object, at any particular time $t$ , equally the derivative of the position with respect to time:

{\boldsymbol {v}}=\lim _{{\Delta t}\to 0}{\frac {\Delta {\boldsymbol {x}}}{\Delta t}}={\frac {d{\boldsymbol {x}}}{dt}}.

From this derivative equation, in the ane-dimensional example it can be seen that the surface area nether a velocity vs. time ( $v$ vs. $t$ graph) is the deportation, $x$ . In calculus terms, the integral of the velocity office $v (t)$ is the displacement function $x (t)$ . In the figure, this corresponds to the yellowish area under the curve labeled $s$ ( $s$ beingness an alternative notation for displacement).

{\boldsymbol {x}}=\int {\boldsymbol {v}}\ dt.

Since the derivative of the position with respect to time gives the alter in position (in metres) divided by the change in fourth dimension (in seconds), velocity is measured in metres per 2d (m/s). Although the concept of an instantaneous velocity might at starting time seem counter-intuitive, it may exist thought of as the velocity that the object would go along to travel at if information technology stopped accelerating at that moment.

Relationship to dispatch

Although velocity is defined equally the rate of change of position, it is often common to start with an expression for an object's acceleration. As seen by the 3 green tangent lines in the figure, an object'due south instantaneous acceleration at a indicate in fourth dimension is the slope of the line tangent to the curve of a $5 (t)$ graph at that point. In other words, acceleration is defined every bit the derivative of velocity with respect to time:

{\boldsymbol {a}}={\frac {d{\boldsymbol {v}}}{dt}}.

From there, nosotros can obtain an expression for velocity every bit the area nether an $a (t)$ dispatch vs. time graph. As to a higher place, this is done using the concept of the integral:

{\boldsymbol {v}}=\int {\boldsymbol {a}}\ dt.

Constant dispatch

In the special example of abiding dispatch, velocity tin be studied using the suvat equations. By considering a as being equal to some capricious constant vector, it is trivial to show that

{\boldsymbol {v}}={\boldsymbol {u}}+{\boldsymbol {a}}t

with $five$ as the velocity at time $t$ and $u$ as the velocity at time $t = 0$ . By combining this equation with the suvat equation $x = u t + a t 2 /2$ , information technology is possible to relate the deportation and the average velocity past

{\boldsymbol {x}}={\frac {({\boldsymbol {u}}+{\boldsymbol {v}})}{2}}t={\boldsymbol {\bar {v}}}t.

Information technology is too possible to derive an expression for the velocity independent of time, known as the Torricelli equation, as follows:

v^{2}={\boldsymbol {v}}\cdot {\boldsymbol {v}}=({\boldsymbol {u}}+{\boldsymbol {a}}t)\cdot ({\boldsymbol {u}}+{\boldsymbol {a}}t)=u^{2}+2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}

(2{\boldsymbol {a}})\cdot {\boldsymbol {x}}=(2{\boldsymbol {a}})\cdot ({\boldsymbol {u}}t+{\tfrac {1}{2}}{\boldsymbol {a}}t^{2})=2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}=v^{2}-u^{2}

\therefore v^{2}=u^{2}+2({\boldsymbol {a}}\cdot {\boldsymbol {x}})

where $v = | v |$ etc.

The above equations are valid for both Newtonian mechanics and special relativity. Where Newtonian mechanics and special relativity differ is in how different observers would describe the aforementioned situation. In particular, in Newtonian mechanics, all observers agree on the value of t and the transformation rules for position create a situation in which all non-accelerating observers would describe the acceleration of an object with the same values. Neither is true for special relativity. In other words, but relative velocity can exist calculated.

Quantities that are dependent on velocity

The kinetic energy of a moving object is dependent on its velocity and is given past the equation

E_{\text{k}}={\tfrac {1}{2}}mv^{2}

ignoring special relativity, where E _k is the kinetic energy and m is the mass. Kinetic energy is a scalar quantity as information technology depends on the foursquare of the velocity, however a related quantity, momentum, is a vector and defined by

{\boldsymbol {p}}=m{\boldsymbol {v}}

In special relativity, the dimensionless Lorentz factor appears frequently, and is given by

\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

where γ is the Lorentz factor and c is the speed of low-cal.

Escape velocity is the minimum speed a ballistic object needs to escape from a massive body such as Earth. It represents the kinetic energy that, when added to the object'due south gravitational potential energy, (which is always negative) is equal to zero. The general formula for the escape velocity of an object at a distance r from the heart of a planet with mass G is

v_{\text{e}}={\sqrt {\frac {2GM}{r}}}={\sqrt {2gr}},

where G is the Gravitational constant and g is the Gravitational acceleration. The escape velocity from World's surface is about eleven 200 yard/s, and is irrespective of the direction of the object. This makes "escape velocity" somewhat of a misnomer, as the more than correct term would be "escape speed": any object attaining a velocity of that magnitude, irrespective of atmosphere, volition leave the vicinity of the base of operations body every bit long every bit it doesn't intersect with something in its path.

Relative velocity

Relative velocity is a measurement of velocity between two objects as determined in a single coordinate system. Relative velocity is fundamental in both classical and modern physics, since many systems in physics deal with the relative move of two or more particles. In Newtonian mechanics, the relative velocity is independent of the chosen inertial reference frame. This is not the case anymore with special relativity in which velocities depend on the choice of reference frame.

If an object A is moving with velocity vector v and an object B with velocity vector west , so the velocity of object A relative to object B is divers equally the deviation of the two velocity vectors:

{\boldsymbol {v}}_{A{\text{ relative to }}B}={\boldsymbol {v}}-{\boldsymbol {w}}

Similarly, the relative velocity of object B moving with velocity w , relative to object A moving with velocity v is:

{\boldsymbol {v}}_{B{\text{ relative to }}A}={\boldsymbol {w}}-{\boldsymbol {v}}

Usually, the inertial frame called is that in which the latter of the two mentioned objects is in rest.

Scalar velocities

In the 1-dimensional instance,^[3] the velocities are scalars and the equation is either:

v_{\text{rel}}=v-(-w)

, if the two objects are moving in opposite directions, or:

v_{\text{rel}}=v-(+w)

, if the two objects are moving in the aforementioned management.

Polar coordinates

Representation of radial and tangential components of velocity at unlike moments of linear movement with abiding velocity of the object around an observer O (it corresponds, for example, to the passage of a car on a straight street around a pedestrian standing on the sidewalk). The radial component can be observed due to the Doppler event, the tangential component causes visible changes of the position of the object.

In polar coordinates, a two-dimensional velocity is described by a radial velocity, defined as the component of velocity away from or toward the origin (also known as velocity fabricated good), and an angular velocity, which is the rate of rotation about the origin (with positive quantities representing counter-clockwise rotation and negative quantities representing clockwise rotation, in a correct-handed coordinate organization).

The radial and angular velocities can exist derived from the Cartesian velocity and displacement vectors by decomposing the velocity vector into radial and transverse components. The transverse velocity is the component of velocity along a circle centered at the origin.

{\boldsymbol {v}}={\boldsymbol {v}}_{T}+{\boldsymbol {v}}_{R}

where

The magnitude of the radial velocity is the dot production of the velocity vector and the unit of measurement vector in the management of the displacement.

v_{R}={\frac {{\boldsymbol {v}}\cdot {\boldsymbol {r}}}{\left|{\boldsymbol {r}}\right|}}

where ${\boldsymbol {r}}$ is deportation.

The magnitude of the transverse velocity is that of the cross product of the unit vector in the direction of the displacement and the velocity vector. It is too the product of the athwart speed $\omega$ and the magnitude of the displacement.

v_{T}={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|}}=\omega |{\boldsymbol {r}}|

such that

\omega ={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|^{2}}}.

Angular momentum in scalar class is the mass times the distance to the origin times the transverse velocity, or equivalently, the mass times the distance squared times the angular speed. The sign convention for athwart momentum is the same equally that for angular velocity.

L=mrv_{T}=mr^{2}\omega

where

The expression $mr^{2}$ is known every bit moment of inertia. If forces are in the radial direction merely with an changed foursquare dependence, equally in the example of a gravitational orbit, angular momentum is constant, and transverse speed is inversely proportional to the distance, angular speed is inversely proportional to the distance squared, and the charge per unit at which area is swept out is constant. These relations are known equally Kepler's laws of planetary motion.

Encounter also

Iv-velocity (relativistic version of velocity for Minkowski spacetime)
Group velocity
Hypervelocity
Stage velocity
Proper velocity (in relativity, using traveler time instead of observer time)
Rapidity (a version of velocity additive at relativistic speeds)
Terminal velocity
Velocity vs. time graph

Notes

^ Rowland, Todd (2019). "Velocity Vector". Wolfram MathWorld. Retrieved 2 June 2019.
^ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale bicentennial publications. C. Scribner's Sons. p. 125. hdl:2027/mdp.39015000962285. Earliest occurrence of the speed/velocity terminology.
^ Basic principle

References

Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June sixteen, 2004). ISBN 0-471-23231-nine.

External links

Wikimedia Eatables has media related to Velocity.

Velocity and Dispatch
Introduction to Mechanisms (Carnegie Mellon University)

vallejoephiculd.blogspot.com

Source: https://en.wikipedia.org/wiki/Velocity